Fourier Methods
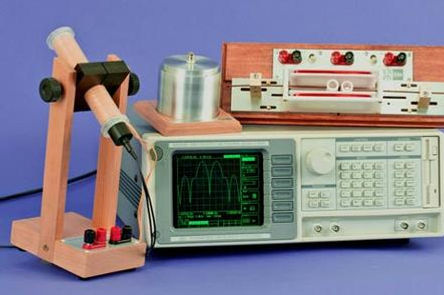
In collaboration with Stanford Research Systems (SRS, Inc.), TeachSpin announces a combination of a high-performance Fourier analyzer (the SR770) and a TeachSpin ‘physics package’ of apparatus, experiments, and a self-paced curriculum. Together, they form an ideal system for students to use in learning about ‘Fourier thinking’ as an alternative way to analyze physical systems. This whole suite of electronic modules and physics experiments is designed to show off the power of Fourier transforms as tools for picturing and understanding physical systems.
Introduction
What are the electronic instrumentation skills that physics students ought to acquire in an undergraduate advanced-lab program? No doubt skills with a multimeter and oscilloscope are basic, and skills with a lock-in amplifier and computer data-acquisition system are more advanced. But our ‘Fourier Methods’ offering adds an intermediate-to-advanced-level and highly-transferable skill set to students’ capabilities. Using it, they can go beyond a passing encounter with the Fourier transform as a mathematical tool in theory courses, to a hands-on benchtop familiarity with Fourier methods in real-time electronic experiments. It represents a skill set that will serve them well in any kind of theoretical or experimental science they might encounter.
The SR770 wave analyzer (shown in the photo) digitizes input voltage signals with 16-bit precision at a 256 kHz rate, and it includes anti-aliasing filters to permit the real-time acquisition of Fourier transforms in the 0-100 kHz range. Any sub-range of the spectrum can be viewed at resolutions down to milli-Hertz. The sensitivity and dynamic range are such that sub-µVolt signals can be displayed with ease, as well as Volt-level signals with signal-to-noise ratio over 30,000:1.
The only additional instruments required to perform these experiments are a digital oscilloscope and any ordinary signal generator. The photo above also shows three ‘hardware’ experiments from TeachSpin: a cylindrical Acoustic Resonator, the Fluxgate Magnetometer in its solenoid, and the mechanical Coupled-Oscillator system. Not shown is an instrument-case full of our ‘Electronic Modules’, which are devised to make possible a host of investigations on the Fourier content of signals.We are confident that the simultaneous use of a ‘scope and the FFT analyzer, viewing the same signal, is the best way to give students intuition for how ‘time-domain’ and ‘frequency-domain’ views of a signal are related. One of our Electronic Modules is a voltage- controlled oscillator (VCO), which can be frequency-modulated by an external voltage. Fig. 1 shows the 770’s view of the spectrum of this VCO’s output, when it is set for a 50-kHz center frequency, with a 1-kHz modulation frequency. This spectrum shows the existence of sidebands, and the frequency ‘real estate’ required by a modulated signal; it also shows that Volt-level signals can be detected standing >90 dB above the noise floor of the instrument.

Fig. 1: Spectrum of frequency-modulated oscillator. Vertical scale is
logarithmic, covering 90 dB of dynamic range (an amplitude ratio of 30,000:1).
As an example of one of our Electronic Modules, let’s consider the LCR-circuit that can be excited by steady sinusoids, by unit-step waveforms, or by the white-noise generator that is built into the SR770. Exciting this one circuit, in turn, by these three signals, students can learn a great deal about the properties of resonant systems. After some point-by-point measurement of the LCR-circuit’s transfer function using sinusoids, they will be impressed to excite its time-domain transient response using a voltage-step waveform, and then seeing the Fourier transform of this transient give the entire spectrum, complete with phase characteristics, all at once in a single shot – see Fig. 2.
Because frequency-mixing technologies are so important across the board in experimental physics, our Electronic Modules include an electronic multiplier, as well as two kinds of mixers. When combined with a ‘local oscillator’ from a signal generator, a signal in any frequency range can be down-shifted into the 0-100 kHz band. Fig. 3 shows a view of part of the AM-radio spectrum, as received in Buffalo, NY. Our modules include all the parts, and all the instructions, to make the audio content of this AM transmission audible through a speaker.

Fig. 2: Real and the imaginary parts of the Fourier transform of an LCR-resonant circuit, excited by a single voltage step and recorded in a single acquisition of duration 64 ms. The spectrum shows the dispersive, and the absorptive, behavior of the resonant system.

Fig. 3: Power spectrum arising from the down-conversion of radio signals. A local oscillator, set to 1113 kHz, is mixed with signals from an antenna, revealing the down-conversion of a station’s frequency of 1080 kHz to a 33-kHz beat note. The sidebands to either side of the down-converted carrier reveal the program content of the AM transmission .
The SR770 includes a high-gain front end making it capable of detecting very weak signals. And because it disperses those signals by frequency content, and permits time-averaging, it is also capable of detecting weak signals that are deeply buried in noise. Our Electronic Modules include a signal-under-noise experiment, in which weak sinusoidal signals are overlaid with analog white noise. Fig.4 shows how such weak signals can be detected by spectral resolution, without the need for a ‘reference signal’ that a lock-in amplifier would require.

Fig. 4: Power spectral density of white noise, showing the presence of a monochromatic signal under the noise. The noise, filtered to the 0-100 kHz bandwidth, has an rms value of 173 mV, and has a 0.83 mV sinusoidal signal contained within it. The spectrum, viewed over a band 97.5 Hz wide, and averaged for 15 seconds, reveals the signal emerging from its burial under noise, and locates it in frequency space.
The noise source in the Modules, and the noise source within the SR770, can both be quantified for spectral noise density, so students will finally be able to use an instrument whose output is calibrated in those mysterious units, Volts/√Hz. They’ll be able to see that the units for measuring the amplitude of spectral peaks (in Volts) and the level of noise floors (in V/√Hz) are incommensurate, and also see that spending more acquisition time will enhance the degree to which a monochromatic signal stands up above the white-noise floor.
Because ‘Fourier methods’ are a set of mental skills transferable to many areas of physics and technology, we have included a set of experiments and projects which showcase the applicability of Fourier analysis:
-
an acoustic resonator, to permit the study of acoustic modes – including finding them all at once by white-noise excitation.
-
fluxgate magnetometer, with a frequency-domain view into its operation, and the ability to detect micro Tesla dc and ac magnetic fields.
-
an electronic analog-computer system which creates the Lorenz attractor, so students can see what chaos looks like, in the time and frequency domains.
-
a unique mechanical coupled-oscillator system, allowing the detection of two resonant modes, and a view of how their mode frequencies can be tuned through an ‘avoided crossing’.
-
inputs for bringing in microphone, and line-input, audio signals, permitting students to see the real-time spectra of sounds they are hearing.
Physicists acquire Fourier-thinking skills in a variety of ways, and apply these skills in many sub-fields of physics. Advanced-lab instructors might want to share, with their theorist colleagues as well as those teaching mechanics, waves & optics and mathematical physics, the capabilities of this Fourier Methods package so that they too can see, and demonstrate for their students, how Fourier analysis works in action.
Instrument
TeachSpin’s ‘Fourier Methods’ initiative represents the strategic combination of several elements:
-
SR770 FFT Spectrum-Analyzer Instrument by Stanford Research Systems
-
TeachSpin Electronic Modules Package
-
Additional External-Hardware Experiments
-
Acoustic Resonator
-
Fluxgate Magnetometer
-
Coupled-Oscillator System
-
-
Instruction Manual with Full Curriculum
Here’s a description of what is included under each of these headings, and how together they provide an unparalleled avenue for students to learn frequency-space thinking.
1. The Stanford Research Systems SR770 is an FFT spectrum analyzer capable of many kinds of Fourier analysis. Its capabilities extend far beyond the FFT function included in some oscilloscopes, and the TeachSpin curriculum has been designed to make full use of those capabilities:
-
16-bit signal quantization, allowing dynamic range in excess of 90 dB (compared to <50 dB for typical 8-bit ‘scope quantization)
-
real-time operation, with full 100-kHz throughput (ie. Fourier-transforms data as fast as it is acquired)
-
precision analog-hardware anti-aliasing filter (permitting 0-100 kHz operation with no fear of spectral aliasing)
-
divisible frequency span, allowing span of 100 kHz or binary sub-multiples (allowing a span as small as 0.192 Hz, and centering such spans anywhere in the 0-100 kHz range)
-
full control of display, window, and averaging modes, including vector averaging for triggered acquisitions
-
front-end full-scale sensitivity of 1 mV, allowing detection of signals of amplitude < 100 nV
-
an internal Source-Out capability, for generating sine, two-tone, noise, and chirp signals of chosen frequency and amplitude
-
storage of set-up and data files in a new USB drive
-
full GPIB and RS-232 access to instrument control and data (for optional computer interfacing)

Simply put, this is a premier instrument, uniquely suited to the teaching, and learning, of Fourier methods. TeachSpin has created both the hardware and curriculum to exploit its full capabilities.
2. The TeachSpin 'Electronic Modules' Package - In one centrally powered box,
TeachSpin’s ‘Electronic Modules’ houses all the building blocks needed to teach
Fourier thinking.
The TeachSpin Physics Module Package Includes:
-
an analog Summer, and a Multiplier, to teach the difference between a
superposition and a product, and to make modulation experiments possible -
two double-balanced Mixers, optimized for Audio and High Frequency bands,
to make demodulation experiments possible -
a Wide-Band Amplifier with 0-2 MHz coverage which can also be used with a
separate AM Antenna module, for one class of radio-detection experiments -
a Power Audio Amplifier and Speaker for various audible effects in Fourier
Methods -
a Voltage Controlled Oscillator (for experiments with frequency-modulation (FM) waveforms, and FM demodulation)
-
a Chaos module - an analog-computer realization of the Lorenz-attractor system for investigating deterministic chaos in time- and frequency-domains
-
a Buried Treasure module, including choices of sinusoidal signals buried under noise for experiments in noise metrology, and signal extraction
-
an L-R-C Circuit, as an example of a linear time-invariant system that can be used as an introduction to the transfer function, and its study by Fourier methods
-
an Intermodulation Distortion module to provide experiments in frequency-space methods for detection of non-linearity
-
a utility Filter module, for high-, low-, and band-pass filtering with various corner frequencies and Q-factors both for study via its transfer function, and as a building block in more complicated assemblies
-
an Audio Connections module that allows students to easily transfer signals between 3.5-mm consumer-market connectors and the BNC-instrumentation world
-
a utility DC Voltage module that can be used with the Summer and Multiplier or Voltage Controlled Oscillator.

3. Three External-Hardware Experiments further expand the range of investigations.

a) an Acoustic Resonator, with speaker and microphone, of cylindrical geometry with fixed diameter but variable length that is used to illustrate the simultaneous detection of a host of normal modes by noise (or chirp) excitation, and Fourier analysis

b) a Fluxgate Magnetometer, with primary-coil excitation, secondary-coil detection, and a special double solenoid for calibration to show the use of non-linear ferromagnetic response as a tool for the detection of µT-level magnetic fields

c) a special Coupled-Oscillator System, of two torsional-reed oscillators that is both magnetically-driven and magnetically-coupled to permit the systematic study of normal-mode behavior in a two-mode system, including the study of the avoided crossing of normal modes
4. Instrument Manual - The educational mission of TeachSpin would be incomplete without a full Instruction Manual teaching the use of all these capabilities. It includes:
Introductory Chapters on:
-
Learning to use a Fourier-transform spectrometer
-
The Source-Out capabilities of the SR770
-
How to produce, and detect, Amplitude Modulation
-
What is Heterodyning, and how does a Mixer do it?
-
How to produce, and detect, Frequency Modulation
-
Quantifying Noise waveforms, and introducing the spectral noise density
-
Studying the LCR system by Fourier methods
-
Transfer functions of Acoustic systems
-
Transient waveforms and their Fourier transforms
Additional Project Experiments which could be performed in any order:
-
Pulse-modulation and its Fourier spectrum
-
Down-conversion and demodulation of AM-radio signals
-
Deterministic chaos, in time- and frequency-domain views
-
The Fluxgate Magnetometer, exploiting harmonic distortion
-
Frequency-domain views of audio waveforms
-
Signal-extraction tactics for signals under noise
-
Coupled oscillators, in theory and experiment
-
Detection of non-linearity by Fourier Methods
-
Demodulation of FM signals
The Manual also contains over a dozen Appendices, where various mathematical, conceptual, and computational issues are addressed. The result is an unmatched resource for teaching, and learning, Fourier methods of calculating and thinking.
Experiments
‘Fourier Methods’ is pre-eminently designed to teach skills in frequency-domain thinking, so our manual includes a long list of skill-building activities. But some of those skills have immediate application to classic experimental techniques, as noted in the projects list below.
Activities:
-
Learning the ropes
-
Superposition
-
Modulations
-
Noise
-
Transfer functions
-
Transient waveforms
Projects:
-
AM radio
-
FM communication
-
Fluxgate magnetometry
-
Couples oscillators
-
Chaos
Activities
1. Learning the ropes
Any FFT analyzer can be thought of as a multi-frequency ac voltmeter, so a first activity is to subject the SR770 to a sinusoidal waveform of variable frequency and amplitude. Seeing a sinusoid, which is continuous in the time domain, show up in the frequency domain. as a delta-function, a single static peak, will help students understand the way FFT analyzer presents information.
2. Superpositions
The Electronic Modules allow the easy creation of a superposition of two sinusoids, one from the 770’s internal generator, and another from any generic signal generator.
The 770 can easily resolve signals that differ by only parts-per-million in frequency. To the right is the spectrum of a superposition of two sinusoidal signals: one is at 50,000.000 Hz, of 100-mV amplitude; the other is at 50,000.282 Hz, of 10-mV amplitude. The 770 not only reveals the frequency difference, less than 6 ppm, it also reveals that one of the oscillators involved is not quite ‘monochromatic’ at this level of frequency resolution.
The 770 can also display signals with amplitudes that differ by a huge factor. Here’s the spectrum of a superposition of frequency components at 50.12 kHz (at 100 mV amplitude) and 51.81 kHz (at 0.001 mV = 1 µV amplitude). The amplitude ratio is 105:1, or 100 dB. The spectrum displayed is the average of 64 spectra, and took less than 4 seconds to acquire.
3. Modulations
Using the Multiplier module, students can set up amplitude-modulated waveforms (using the 770’s internal source as ‘carrier’, and a generic signal generator as ‘signal’ source). They will see that the frequency spectrum of an AM wave is no longer a delta-function, but now has sidebands. This also points out the spectral bandwidth that any information-carrying signal must take up.
Using the VCO module, students can similarly set up frequency-modulated waveforms. Here, they will see that an FM waveform’s spectrum contains multiple sidebands, with magnitudes given by a Bessel-function expansion. They will also see that a carrier, whose frequency is modulated continuously in time, nevertheless will display a spectrum with discrete sidebands.


4. Noise
Students can use the Noise module to see noise waveforms in the time and frequency domains. They can also learn the connection between a noise signal’s rms measure (in the time domain) and its noise spectral density (in the frequency domain). They can learn the quantitative significance of the units V2/Hz and V/√Hz as appropriate units for noise.
Students can also learn how to use the 770 for the ‘blind detection’ of a weak sinusoidal signal buried under broadband noise. In the process, they’ll see how it is that a lock-in amplifier can work, but with the advantage of seeing how a signal peak can be made to stand up above a ‘noise floor’.
5. Transfer functions
With noise waveforms modeled and measured as superpositions of sinusoids, students are now ready to see the usefulness of noise as an excitation source for systems. Fourier Methods includes an Acoustic Resonator, and an electronic LCR Circuit, as model linear systems. Each can have its behavior investigated by traditional one-frequency-at a-time, generator-and-oscilloscope methods. But each can alternatively have its entire frequency spectrum acquired ‘all at once’, in a lovely illustration of how Fourier methods are actually used in so many forms of spectroscopy.
To the right shows the spectrum of pick-up from a microphone in the Acoustic Resonator, when the speaker exciting that resonator is driven by a quasi-noise ‘chirp’ waveform. The entire spectrum, showing a whole collection of resonant modes, can be acquired afresh every 32 ms.

6. Transient waveforms
The SR770 allows the triggered acquisition of transient waveforms. Since this triggering establishes a t = 0 definition, it also permits the derivation of phase information in Fourier spectra. Students can learn the value of magnitude & phase, or alternatively, real & imaginary parts, in the depiction of spectra and of transfer functions. They can also learn how averaging of results from repeated pulsed excitation of transients allows powerful noise-reduction techniques.
Projects
In Fourier Methods we have included some hardware apparatus especially suited to projects illustrating the conceptual value of Fourier thinking.
1. AM Radio
Using almost any available signal generator as a ‘local oscillator’, students can use the external Antenna structure included in the apparatus and a whole assembly of Electronic Modules to understand, systematically, the process of down-conversion and de-modulation. They will not only be able to hear live AM radio broadcasts on a speaker, but they will also understand the roles of amplification, mixing, filtering, and detection in the process.
2. FM Communication
When studying Modulation in section 3 of Activities, students learn how a signal waveform can be ‘encoded’ by its action in frequency-modulating a carrier. Then, using the Electronic Modules, including crucially the phase response of an LCR circuit, students can de-modulate an FM waveform, and thereby ‘decode’ the original signal information.
3. Fluxgate magnetometry
While a Fourier analyzer is sometimes used to detect and quantify undesired ‘harmonic distortion’, there are places in physics where the harmonics generated by non-linearity are the desired outcome. So it is with a Fluxgate Magnetometer, in which external dc (or ac!) magnetic fields, even at the µT (0.01 gauss) level, can be detected via the non-linearity they help to create in ac-excited ferromagnetic materials. Students will learn a real-life application of the triad of fields B, H, and M, and learn how to operate and calibrate a magnetic-field sensor based on these properties.
4. Coupled oscillators
Many linear systems can be understood via their spectrum of normal modes, so we’ve provided a system of two mechanical oscillators which allows the systematic study of a two-mode system. Our Coupled-Oscillator System has adjustable magnetic coupling of the two oscillators, and separately-adjustable tuning of the two oscillators’ frequencies. Both oscillators can be excited or detected by ac electrical means, so this coupled-oscillator system can be studied via its Fourier spectrum in real time. We have optimized the system to permit the detection of the ‘avoided crossing’ of two normal-mode frequencies, to introduce students to this widely-encountered phenomenon.
To the right is the response to electrical stimulation of our coupled-oscillator system, again obtained all-at-once using chirp excitation. The two major peaks locate the system’s two normal modes, and this spectrum gives the frequencies of both modes to <0.1-Hz precision. It’s those two normal-mode frequencies which undergo an ‘avoided crossing’ in response to a tuning parameter.

5. Chaos
One of the revelations in physics in recent times has been to see apparent randomness arising from wholly deterministic systems. The ‘chaos revolution’ broke into physicists’ consciousness with the properties of the Lorenz attractor, derived from fluid mechanics and modeled by a set of three fully-deterministic, first-order, but non-linear differential equations. The electronic modules of Fourier Methods include an electronic analog-computer realization of this Lorenz system, so students have real-time access to three chaotically-oscillating voltages. But in the Fourier-Methods environment, they can also, and simultaneously, view any of these signals in the frequency domain. Because the Lorenz system can be tuned into, or out of, regimes of periodicity surrounded by chaotic behavior, observing this phenomenon in the frequency domain allows especially clear insight into the quite general feature of the ‘period-doubling route to chaos’

While our Lorenz-attractor module gives a continuous frequency spectrum when in its chaotic mode, it can also be adjusted into a regime of periodic output. In such a case, the Fourier spectrum collapses from a continuum into a series of harmonically-related spectral lines.

Then a small adjustment of the Lorenz system’s r-parameter will change its behavior into a period-doubled regime. Here, the Fourier spectrum is still a harmonic series of spectral lines, but a new, and lower-frequency, spectral line has emerged. So the fundamental frequency is about half, ie. the period is about double, compared to the previous behavior.
